简单diff算法
9.1 减少DOM操作的性能开销
当新旧子节点都为数组的时候。需要进行核心diff算法,最暴力的当然是将全部旧子节点卸载,新节点挂载上。
当然还有大家可以简单想到的办法就是将新旧子节点数组的共同长度做patch,然后进行考虑新节点新增与删除的情况。
例如以下新旧节点
// 旧vnode
const oldVNode = {
type: 'div',
children: [
{type: 'p', children: '1'},
{type: 'p', children: '2'},
{type: 'p', children: '3'}
]
}
// 新vnode
const newVNode = {
type: 'div',
children: [
{type: 'p', children: '4'},
{type: 'p', children: '5'},
{type: 'p', children: '6'}
]
}
diff算法如下
/**
n1: 旧节点
n2: 新节点
container: 真实dom
*/
function pathChildren(n1, n2, container) {
const oldChildren = n1.children
const newChildren = n2.children
// 新旧子节点都为数组的情况
const oldLen = oldChildren.length
const newLen = newChildren.length
const commonLen = Math.min(oldLen, newLen)
for(let i = 0; i < commonLen; i++) {
path(oldChildren[i],newChildren[i],container)
}
if(newLen > oldLen) {
for(let i = commonLen; i < newLen; i++) {
path(null, newChildren[i], container)
}
}else if(oldLen > newLen) {
for(let i = commonLEn; i < oldLen; i++) {
unmount(oldChildren[i])
}
}
}
9.2 DOM复用与key的作用
以上考虑的是没有新子节点没有移动的情况,加入有移动的情况的情况,则以上简单的算法不能满足,比如
// oldChildren
[
{type: 'p', children: '1'},
{type: 'p', children: '2'},
{type: 'p', children: '3'}
]
// newChildren
[
{type: 'p', children: '3'},
{type: 'p', children: '1'},
{type: 'p', children: '2'}
]
如果考虑了移动的情况,则根据type类型是否相同判断是否需要更新则满足不了需求(之前根据type相同则进行patch,否则卸载旧节点,挂载新节点)。加入key后新旧子节点如下。
// oldChildren
[
{type: 'p', children: '1', key: 1},
{type: 'p', children: '2', key: 2},
{type: 'p', children: '3', key: 3}
]
// newChildren
[
{type: 'p', children: '333', key: 3},
{type: 'p', children: '111', key: 1},
{type: 'p', children: '222', key: 2}
]
这样通过遍历新节点数组,找出在旧节点数组中相同的key进行patch
function patchChildren(n1, n2, container) {
const oldChildren = n1.children
const newChildren = n2.children
for (let i = 0; i < newChildren.length; i++) {
const newVNode = newChildren[i]
for (let j = 0; j < oldChildren.length;j++) {
const oldVNode = oldChildren[j]
if(newVNode.key === oldVNode.key) {
patch(oldVNode,newVNode,container)
break;
}
}
}
}
经过上面patch之后旧的oldChildren已变为
[
{type: 'p', children: '111', key: 1},
{type: 'p', children: '222', key: 2},
{type: 'p', children: '333', key: 3}
]
但是此时oldChildren对应的位置还没有更新。此时,需要进行移动操作
9.3 找到需要移动的元素
怎么找到移动的元素?
简单观察即可知道当新旧节点key值相等的时候,并且新旧节点的下标相同的时候不需要更新。并且新节点的下标是递增的,则不需要移动。
接下来考虑:假如有移动的情况呢?则可以想到出现不是递增的话就会出现移动的情况,但怎样判断?只需要定义一个变量,记录当key相同时,新vnode在旧vnode中位置的出现最大的下标位置即可。如果当前位置小于最大的下标位置则认为需要移动。如下图
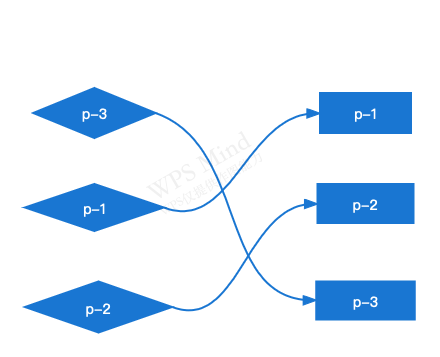
- p-3 新节点对应旧子节点下标为2,此时最大下标为初始值0,大于初始值,则不进行移动同时最大下标更新为2
- p-1 新节点对应旧子节点下标为0,此时最大下标为2,小于最大下标,需要移动
- p-2 新节点对应旧子节点下标为1,此时最大下标为2,小于最大下标,需要移动
function patchChildren(n1, n2, container) {
const oldChildren = n1.children
const newChildren = n2.children
let maxIndex = 0
for (let i = 0; i < newChildren.length; i++) {
const newVNode = newChildren[i]
for (let j = 0; j < oldChildren.length;j++) {
const oldVNode = oldChildren[j]
if(newVNode.key === oldVNode.key) {
patch(oldVNode,newVNode,container)
if(j < maxIndex) {
// 需要移动
} else {
maxIndex = j
}
break;
}
}
}
}
9.4 如何移动元素
移动的话其实根据就是将旧dom根据新节点的位置移动到新子节点的后面。
就是遍历新节点,然后移动旧节点即可,在上面代码基础上增加移动操作。
其中真实dom是存在VNode的el字段中
function patchChildren(n1, n2, container) {
const oldChildren = n1.children
const newChildren = n2.children
let maxIndex = 0
for (let i = 0; i < newChildren.length; i++) {
const newVNode = newChildren[i]
for (let j = 0; j < oldChildren.length;j++) {
const oldVNode = oldChildren[j]
if(newVNode.key === oldVNode.key) {
patch(oldVNode,newVNode,container)
if(j < maxIndex) {
// 需要移动
// 9.4 找到新子节点的前一个节点
const preVNode = newChildren[i-1]
// 如果前一个节点为真才需要移动,否则的话就是第一个节点,不需要移动
if(preVNode) {
// 获取前一个节点的下一个兄弟节点作为锚点
const anchor = preVNode.el.nextSibling
// 调用dom的insert方法
insert(newVNode.el,container, anchor)
}
} else {
maxIndex = j
}
break;
}
}
}
}
9.5 添加新元素
假如新节点中有新增的情况,需要进行挂载,因为只需要增加一个布尔变量表示新子节点在旧子节点中是否找到即可。没找到挂载就行。
// 在第一个for循环内定义变量 let find = false。在第二个for循环内找到相同的key话 find = true
// 在第二个for循环后面增加新增情况
if(!find) {
// 找到前一个节点
const preVNode = newChildren[i-1]
let anchor = null
if(preVNode) {
anchor = preVNode.el.nextSibling
} else {
anchor = container.firstChild
}
// 挂载 newVNode
patch(null, newVNode, caontainer, anchor)
}
9.6 删除不存在的元素
因为是通过遍历新节点数组来找旧节点数组中对应的节点,因为以上代码会漏掉不存在的旧节点。
-
可以通过再次遍历旧节点数组,看是否在新节点数组中存在,如果在新节点数组中没有存在说明需要删除。
-
因为此前已经双重遍历过了,也可定义一个set将所有旧节点放在set中,如果在新节点找到了就删除掉,剩下没有被删除的就是在新节点中不存在需要删除的节点。代码如下。
function patchChildren(n1, n2, container) {
const oldChildren = n1.children
const newChildren = n2.children
let maxIndex = 0
let oldChildrenSet = new Set()
for (let i = 0; i < newChildren.length; i++) {
const newVNode = newChildren[i]
for (let j = 0; j < oldChildren.length;j++) {
const oldVNode = oldChildren[j]
// 只用第一轮中将所有的旧节点添加到set中即可
if(i === 0) {
oldChildrenSet.add(oldVNode)
}
if(newVNode.key === oldVNode.key) {
// 将旧节点从set中删除
oldChildrenSet.delete(oldVNode)
patch(oldVNode,newVNode,container)
if(j < maxIndex) {
// 需要移动
// 9.4 找到新子节点的前一个节点
const preVNode = newChildren[i-1]
// 如果前一个节点为真才需要移动,否则的话就是第一个节点,不需要移动
if(preVNode) {
// 获取前一个节点的下一个兄弟节点作为锚点
const anchor = preVNode.el.nextSibling
// 调用dom的insert方法
insert(newVNode.el,container, anchor)
}
} else {
maxIndex = j
}
break;
}
}
}
// 遍历旧节点的set,然后卸载即可
oldChildrenSet.forEach(v => umount(v))
oldChildrenSet.clear()
}

